18 직선으로의 정사영
18.1 직선으로의 사영
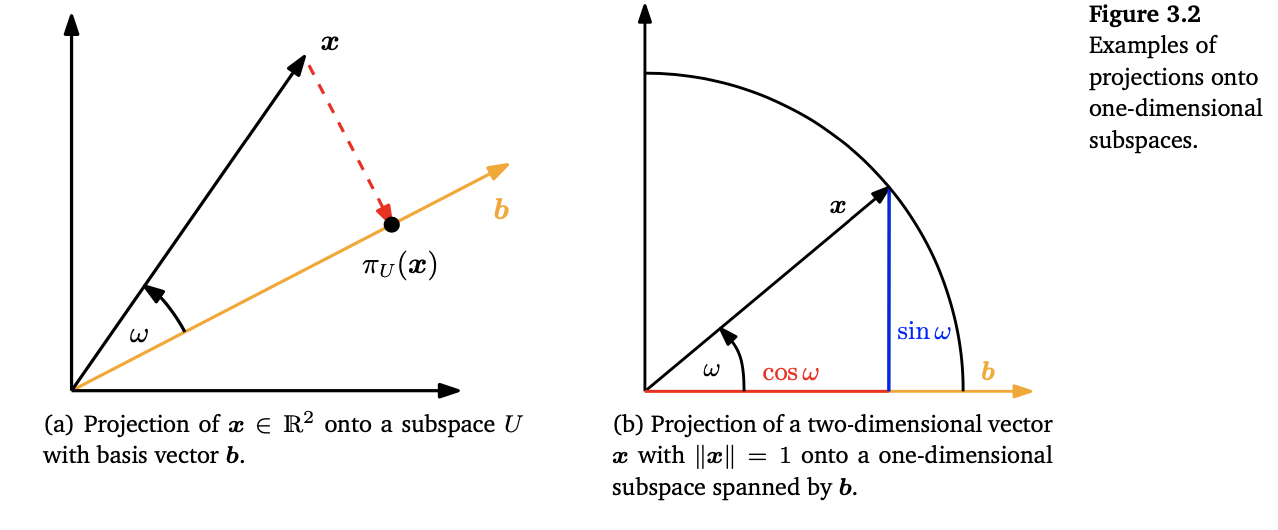
- 벡터 \(\pmb b\) 의 방향과 같은 벡터들 중에 벡터 \(\pmb x\) 와 가장 가까운 벡터를 \(\pi_U(\pmb x)\) 라고 하자. 이 벡터는 \(\pmb x\) 에서 직선 \(\pmb b\) 에 내린 사영(projection)이며 다음을 만족해야 한다.
\[ \left\langle\pmb{x}-\pi_U(\pmb{x}), \pmb{b}\right\rangle=0 \tag{18.1}\]
- 사영 \(\pi_U(\pmb x)\) 는 벡터 \(\pmb b\) 의 방향이므로 어떤 스칼라 \(\lambda\) 가 존재하여 다음을 만족해야 한다.
\[ \pi_U(\pmb{x})=\lambda \pmb{b} \]
- 식 18.1 에서 제시된 직교하는 성질을 다시 쓰면 조건과 같다.
\[ \langle\pmb{x}-\lambda \pmb{b}, \pmb{b}\rangle=0 . \]
- 내적의 성질을 이용하면 다음을 얻을 수 있다. \[ \langle\pmb{x}, \pmb{b}\rangle-\lambda\langle\pmb{b}, \pmb{b}\rangle=0 \Longleftrightarrow \lambda=\frac{\langle\pmb{x}, \pmb{b}\rangle}{\langle\pmb{b}, \pmb{b}\rangle}=\frac{\langle\pmb{b}, \pmb{x}\rangle}{\|\pmb{b}\|^2} . \] 따라서 스칼라 \(\lambda\) 는 다음과 같다.
\[ \lambda=\frac{\pmb{b}^{\top} \pmb{x}}{\pmb{b}^{\top} \pmb{b}}=\frac{\pmb{b}^{\top} \pmb{x}}{\|\pmb{b}\|^2} \]
- 이제 벡터 \(\pmb b\) 의 방향으로의 벡터 \(\pmb x\)의 사영 \(\pi_U(\pmb x)\) 는 다음과 같다.
\[ \pi_U(\pmb{x})=\lambda \pmb{b}=\frac{\langle\pmb{x}, \pmb{b}\rangle}{\|\pmb{b}\|^2} \pmb{b}=\frac{\pmb{b}^{\top} \pmb{x}}{\|\pmb{b}\|^2} \pmb{b} \tag{18.2}\]
- 식 18.2 에서 \(\pmb{b}^{\top} \pmb{x}\) 는 스칼라이므로 다음과 같이 쓸 수 있으며 노름(norm)의 정의와 행렬의 결합법칙을 이용하면 다음과 같다.
\[ \begin{aligned} \pi_U(\pmb{x}) &= \frac{\pmb{b}^{\top} \pmb{x}}{\|\pmb{b}\|^2} \pmb{b} \\ & = \pmb{b} \frac{\pmb{b}^{\top} \pmb{x}}{\|\pmb{b}\|^2} \quad (\text{스칼라 성질을 이용})\\ & =\frac{\pmb{b} (\pmb{b}^{\top} \pmb{x})}{\pmb{b}^{\top} \pmb{b}} \\ & =\frac{(\pmb{b} \pmb{b}^{\top}) \pmb{x}}{\pmb{b}^{\top} \pmb{b}} \quad (\text{결합법칙을 이용})\\ & =\frac{\pmb{b} \pmb{b}^{\top}}{\pmb{b}^{\top} \pmb{b}} \pmb{x} \\ & =\frac{\pmb{b} \pmb{b}^{\top}}{\|\pmb{b}\|^2} \pmb{x} \\ & =\pmb P_{\pi}\pmb{x} \end{aligned} \]
- 벡터 \(\pmb b\) 의 방향으로 사영행렬 \(\pmb P_{\pi}\) 는 다음과 같다.
\[ \pmb P_{\pi} = \frac{\pmb{b} \pmb{b}^{\top}}{\|\pmb{b}\|^2} \tag{18.3}\]
식 18.3 에서 \(\pmb{b} \pmb{b}^{\top}\) 는 정방행렬이고 \(\|\pmb{b}\|^2\)는 스칼라임에 유의하자.
이미 사영된 \(\pi_U(\boldsymbol{x})\) 에 다시 사영행렬 \(\boldsymbol{P}_\pi\) 을 곱해도 아무런 변화가 없다. 이는 벡터 \(\pmb x\) 를 이미 벡터 \(\pmb b\) 의 방향으로 사영했기 때문에 다시 사영해도 변화가 없다는 것을 의미한다.
즉, \(\boldsymbol{P}_\pi \pi_U(\boldsymbol{x})=\pi_U(\boldsymbol{x})\) 이다. 사영행렬 \(\boldsymbol{P}_\pi\) 가 모든 벡터 \(\boldsymbol{x}\) 에 대해 \(\boldsymbol{P}_\pi^2 \boldsymbol{x}=\boldsymbol{P}_\pi \boldsymbol{x}\) 를 만족한다는 것을 의미한다.
\[ \boldsymbol{P}_\pi^2 = \boldsymbol{P}_\pi \]
18.2 중요한 내용과 정의
- 슬라이드 18번의 5페이지에 나온 사영행렬에 대한 예제
- 부교재 Example 3.10