13  선형변환의 핵과 상

13.1 핵과 상의 정의

정의 13.1 (선형변환의 핵과 상) 벡터공간 \(V\), \(W\) 사이의 선형사상 \(T :V \rightarrow W\)를 고려하자. 선형사상 \(T\) 의핵(kernel) \(Ker(T)\) 또는 영공간(null space) \(N (T )\) 는 다음과 같이 정의된다:

\[ ker(T) = N (T ) = \{ \pmb v \in V \mid T( \pmb v) = \pmb 0 \} \]

또한 선형사상 \(T\) 의 상(range) 또는 치역(image) \(Im(T)\) 는 다음과 같이 정의된다:

\[ Im(T) = T(V) = \{ T(\pmb v) \mid \in V \} \]

---

선형변환의 핵과 상

---

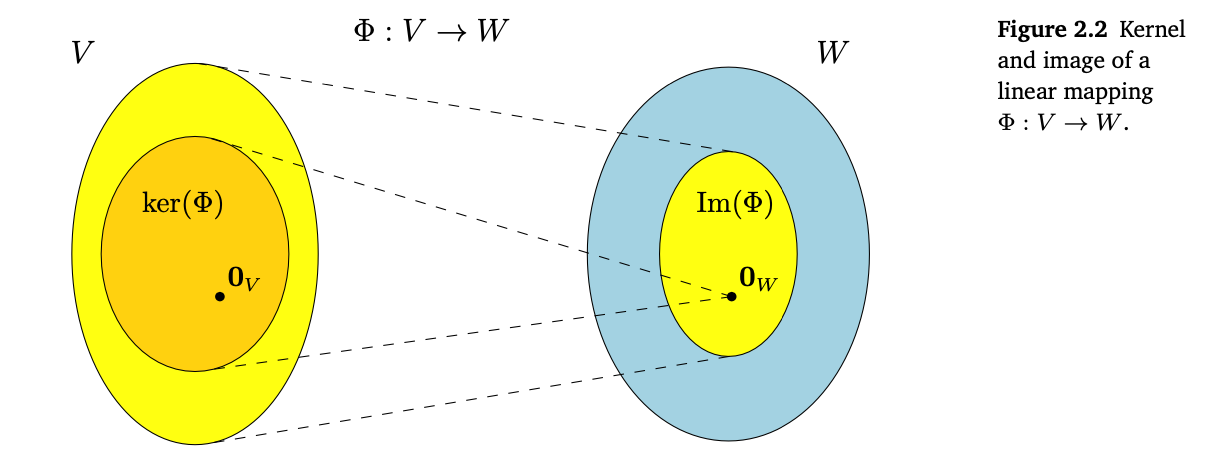
13.1.1 예제

• 부교재 Example 2.25 (Image and Kernel of a Linear Mapping)