5.3. 확률과 컴퓨터 실험#

5.3.1. 우연성과 가능성#

이 절에서는 우연성(randomness)에 대하여 조금 더 알아보자.

우리가 “오늘 친구와 우연히 만나서 즐겁게 놀았다” 라고 말하면 이 문구에서 “우연히”라는 단어는 의도하지 않은 사건이 발생했다는 의미이다. “우연” 은 사전적으로 “아무런 인과 관계가 없이 뜻하지 아니하게 일어난” 이라는 의미로 사용된다.

이 강의에서 말하는 우연성(randomness) 이란 인과 관계가 없다는 의미보다 특정한 사건의 결과를 미리 정확하게 예측할 수 없는 경우를 말한다. 우연성을 다른 말로는 임의성, 랜덤, 무작위, 확률적 이라고 표현한다.

다음은 사건의 결과가 우연성을 가진 예들이다.

  • 동전을 던질 때 결과

  • 주사위를 던질 때 결과.

  • 가위, 바위, 보 게임에서 내가 이긴다.

  • 이번 주 토요일 내가 산 복권이 당첨된다.

또한 아래 질문에서도 그 결과를 정확하게 예측하기 힘들다.

  • 이번 주말에 캠핑 가기로 했는데 비가 올까?

  • 내일 내가 투자한 주식이 상종가를 칠까? :)

물론 예측하는 능력에 따라서 비가 올지, 투자한 주식이 오를지에 대한 “가능성”을 잘 예측하여 결과를 맞출 수도 있겠지만 틀릴 경우도 많다는 사실을 여러분들은 더 잘 알고 있을 것이다. 따라서 비가 올지, 주식의 가격이 올라갈 지 정확하게 예측할 수 없다.

참고로 동전 던지기의 우연성에 대한 재미난 비디오를 보고 결과의 예측에 대하여 생각해 보자.

5.3.2. 확률과 컴퓨터 실험#

어떤 사건의 결과가 우연성을 가지고 있어서 미리 그 결과를 정확하게 예측할 수 없지만 가능한 결과들의 가능성 에 대해서는 믿을 만한 합리적 지식을 가지고 잇는 경우가 있다.

예를 들어서 여러분이 친구와 동전을 던져서 내기를 하는 경우 앞면과 뒷면이 나올 가능성이 같을 것이라고 믿는다. 마찬가지로 주사위를 던져서 게임을 하는 경우도 6개의 숫자가 나올 가능성은 모두 같을 것(equally likely)이라고 믿는다. 가능성이 같지 않다고 믿는다면 여러분은 내기에 응하지 않을 것이다.

통계학에서 이러한 가능성을 나타내는 측도를 확률(probability) 라고 한다.

동전을 던져서 내기를 하는 경우 앞면과 뒷면이 나올 확률은 각각 1/2 이며 주사위를 던져서 게임을 하는 경우도 6개의 숫자가 나올 확률은 각각 1/6 이다.

  • 만약 나올 수 있는 가능한 결과들을 미리 알고 있으며(보통 우리는 동전이 눕지 않고 서 있을 거라고 예상하지 않는다)

  • 결과에 대한 가능성을 미리 알고 있다면 (동전의 앞면이 나올 확률을 알고 있다면)

우리는 컴퓨터 프로그램을 이용하여 사건의 결과에 대한 유용한 정보를 얻을 수 있다.

컴퓨터를 이용하여 같은 사건을 반복해서 실행하면 가능한 결과들의 분포에 대한 정보를 얻을 수 있는 것이다. 이러한 것을 컴퓨터 실험(computer experiment, simulation) 이라고 한다.

5.3.3. 난수#

import pandas as pd
import numpy as np

컴퓨터가 할 수 있는 다양한 기능들 중에 숫자를 임의로 선택해 주는 기능은 매우 유용하고 중요한 기능이다.

“임의로 선택해 준다”는 의미는 주어진 수들의 집합에 있는 모든 수가 선택될 가능성이 같다는 의미(equally likely)이다. 주어진 수들의 집합에서 컴퓨터가 눈을 감고 뽑아준(^^) 수를 난수(random number) 라고 말한다.

물론 컴퓨터가 스스로 알아서 난수를 뽑아주는 것은 아니고 사람이 난수를 발생시키는 알고리즘을 프로그램으로 구현해 놓았기 떄문에 이런 기능을 이용할 수 있다.

컴퓨터가 난수를 선택해 주는 일을 수행할 때 가장 기본적인 작업은 0과 1 사이에서 하나의 실수(floating point)를 눈 감고 뽑아주는 기능이다.

아래 함수 np.random.rand(n)은 n 개의 실수를 0과 1사이 에서 임의로 선택해 준다. 여러분들이 아래 코드를 여러 번 반복해서 실행시켜 보면 코드가 실행될 때마다 컴퓨터가 임의로 선택해준 값이 다르게 나오는 것을 볼 수 있다.

함수 np.random.rand(n)의 결과는 길이가 n 인 실수 벡터이다.

np.random.rand(1)

array([0.16955076])

np.random.rand(5)

array([0.24652516, 0.33276944, 0.7919059 , 0.61695644, 0.59237238])

5.3.4. 조건문#

위에서 동전을 던지는 경우 결과는 우연성을 가진다고 배웠다. 이제 우리는 컴퓨터가 우리를 위하여 공정한 동전(fair coin)을 던져서 그 결과를 주는 코드를 작성해 볼 것이다.

동전을 던지는 경우 가능한 결과가 앞면 과 뒷면 이고 두 결과의 가능성이 같다는 것을 어떻게 컴퓨터에게 알려줘야 할까? 앞에서 배운대로 컴퓨터가 0 보다 크고 1 보다 작은 모든 실수 집합에서 하나의 난수를 임의로 뽑아줄 수 있다면 뽑힌 수가 0.5보다 작을 가능성은 0.5보다 클 가능성과 같다.

따라서 함수 np.random.rand(1) 로 뽑힌 난수가 0.5 보다 작으면 앞면, 0.5 보다 크면 뒷면 으로 결과를 주면 공정한 동전을 던지는 실험을 구현할 수 있다.

5.3.4.1. 조건문의 구조#

프로그램 언어에서 주어진 조건에 따라서 다른 결과를 주는 명령어 를 조건문(conditional statement) 이라고 한다. 파이썬 조건문은 다음과 같은 문법을 따른다.

if 조건 1 :
  결과 1
  ...
elif 조건 2 :
  결과 2
  ...
elif 조건 3 :
  결과 3
  ...

...

elif 조건 k :
  결과 k
  ...
else  :
  결과
  ...

위의 코드는 k 개의 조건(조건 1, 2, …, k)을 순서대로 검사하여 참인 경우 해당하는 결과만을 실행하는 조건문의 일반적인 형태이다

  1. 먼저 처음 if 뒤 조건 1 의 결과가 참(True)이면 결과 1 ...을 수행하고 다른 조건에 대한 판단없이 끝이 난다. 조건 1 의 결과가 거짓(False)이면 아래 코드 elif 로 넘어간다.

  2. 코드 elif 뒤 조건 2 의 결과가 참(True)이면 결과 2 ...을 수행하고 다른 조건에 대한 판단없이 끝이 난다. 조건 2 의 결과가 거짓(False)이면 아래 코드 elif 로 넘어간다.

  3. 이렇게 순서대로 조건을 검사하여 주어진 조건이 참인 경우 해당하는 결과만 실행하며 모든 조건이 거짓인 경우 코드 else 문 뒤에 나온 결과 ... 를 실행한다.

주의할 점

  1. 각 결과를 실행하는 명령문들은 if, elif, else 문보다 최소한 공백 하나만큼 들여쓰기 해야 한다. 들여쓰기한 명령문들을 블럭(block)이라고 한다.

  2. if, elif, else 문에서 조건이 끝나는 것을 반드시 : 으로 표시해 준다.

참고로 elif는 else if 의 줄임말이다.

5.3.4.2. 공정한 동전 던지기#

공정한 동전(fiar coin)을 던지는 실험을 수행하는 간단한 코드를 작성해 보자. 난수의 값이 0.5 보다 작으면 앞면 을 출력하고, 아니면(0.5 보다 크면) 뒷면을 출력하는 조건문의 예이다.

아래 코드를 여러 번 반복해서 실행시키면서 난수 x 의 값과 동전 던지기의 결과를 보자.

x = np.random.rand(1)
print(x)

if x < 0.5 :
 print("앞면")
else :
 print("뒷면")    

[0.55630756]
뒷면

주의할 사항은 조건에 따라서 실행되는 결과 코드, 즉 print() 문은 if 문에서 최소한 한 줄씩 들여쓰기 해야한다.

다음과 같이 들여쓰기를 하지 않으면 오류가 발생한다

x = np.random.rand(1)
print(x)

if x < 0.5 :
print("앞면")
else :
print("뒷면") 

  File "<ipython-input-5-9b2187854a0a>", line 5
    print("앞면")
        ^
IndentationError: expected an indented block

5.3.4.3. 공정하지 않은 동전#

이제 앞면이 나올 가능성이 뒷면보다 2배가 큰 공정하지 않은 동전을 던지는 실험을 구현해 보자.

(0,1)을 균등하게 새 구간 (0,1/3), (1/3,2/3), (2/3,1) 으로 나누고 난수의 결과가 첫 번째와 두 번째 구간에 속하면, 즉 난수가 2/3 보다 작으면 앞면, 2/3 보다 크면 뒷면이 나오도록 하면 된다.

x = np.random.rand(1)
print(x)

if x < 2/3 :
  print("앞면")
else :
  print("뒷면")    

[0.29124044]
앞면

5.3.5. 반복#

위에서 구현한 동전 던지기 실험을 여러 번 반복해서 수행할 수는 없을까?

프로그램 언어에서 같은 작업을 여러 번 반복하여 실행하는 기능 을 loop 라고 한다.

5.3.5.1. 반복문의 구조#

만약 주어진 코드들을 n 번 반복하여 실행하고 싶다면 다음과 같이 for ... in ... 명령문을 사용한다.

for target in iterable_object :
  코드 1
  코드 2
  ...

명령문 for 뒤에는 반복하면서 순서대로 뽑히는 것을 저장할 target 변수를 지정하고 in 뒤에는 반복할 것들이 나열되어 있는 대상(iterable_object)을 지정해 준다. 조건문과 마찬가지로 명령문 for 다음에 나오는 반복할 명령문들(블럭)은 최소한 공백 하나로 들여쓰기 해야 한다.

예를 들어서 0부터 9까지의 정수로 구성된 벡터의 원소를 차례대로 프린트하는 반복문은 다음과 같이 쓸 수 있다. for 문 뒤에 나오는 i 변수는 반복에 따라서 my_iter1의 원소로 차례대로 지정된다.

my_iter1 = np.arange(10)

for i in my_iter1 :
  print(i)

0
1
2
3
4
5
6
7
8
9

위의 코드는 아래와 같이 더 간단하게 쓸 수 있다.

for i in np.arange(10) :
  print(i)

0
1
2
3
4
5
6
7
8
9

다음과 같이 반복문을 사용하여 1부터 10 까지 숫자의 합을 구할 수 있다.

  1. 먼저 1부터 10 까지 저장된 반복할 벡터 mynumbers 를 만들고

  2. 반복문을 사용하기 전에 먼저 숫자의 합을 저장할 변수 mysum의 값을 0 으로 지정하고

  3. 반복문 for 를 사용하여 매 반복마다 꺼낸 숫자 i 를 mysum 에 더해준다.

mynumbers = np.arange(1,11) ## 1부터 10까지 저장된 벡터 - 끝나는 숫자기 11인것에 유의하다.

mysum = 0

for i in mynumbers :
  mysum = mysum + i

mysum

55

반복할 것들이 나열되어 있는 대상은 다음과 같이 문자로 된 벡터도 가능하다.

my_iter2 = [ "A", "B", "C", "D"]

for i in my_iter2 :
  print(i)

A
B
C
D

반복분은 다음과 같이 중첩해서 사용할 수 있다. 바깥 쪽에 있는 반복문에서 i가 먼저 정해진 후에 안쪽에 있는 j가 반복된다.

for i in np.arange(5) :
  for j in np.arange(3) :
    print(i,j)

0 0
0 1
0 2
1 0
1 1
1 2
2 0
2 1
2 2
3 0
3 1
3 2
4 0
4 1
4 2

5.3.5.2. 동전 던지기의 반복#

이제 위에서 동전을 던지는 코드를 10회 반복해 보자.

여러분이 아래 명령문 for i in np.arange(10) 에서 10을 다른 숫자로 바꾸면, 예를 들어 100으로 바꾸면 100번 동전을 던진 결과가 출력될 것이다.

for i in np.arange(10) :
  x = np.random.rand(1)
  print(x)

  if x < 0.5 :
    print("앞면")
  else :
    print("뒷면")    

[0.39814955]
앞면
[0.1849489]
앞면
[0.07670611]
앞면
[0.11136791]
앞면
[0.36775051]
앞면
[0.97752369]
뒷면
[0.1695659]
앞면
[0.00365524]
앞면
[0.28785766]
앞면
[0.74082434]
뒷면

5.3.6. 확률 실험#

실험(experiment)은 주어진 여러 가지 조건과 우연성에 대한 정보를 이용하여 원하는 사건를 반복해서 실행하는 것이다.

실험은 다른 말로 모의실험(simulation)이라고 부르며 특별히 우연성, 즉 확률을 이용한 실험을 확률 실험(stochastic experiment, stochastic simulation) 이라고 한다.

5.3.6.1. 동전 던지기#

이제 위에서 배운 조건문과 반복분을 이용하여 다음과 같은 질문에 대한 답을 구해보자.

  • 공정한 동전을 1000번 던졌을 때 앞면이 나올 횟수는?

위의 질문에 대답하기 위해서

  • 실험의 시작 전에 앞면이 나오는 횟수을 세는 변수 count_head 를 0 으로 지정한다.

  • 각 반복마다 앞면이 나오는 경우 count_head 의 값을 1씩 증가시킨다.

다음은 공정한 동전을 1000번 던졌을 (N=1000) 때 앞면이 나올 횟수를 count_head 에 저장하는 코드이다.

N = 1000
count_head = 0

for i in np.arange(N) :

  x = np.random.rand(1)

  if x < 0.5 :
    count_head = count_head + 1

count_head

510

주의할 점

  1. 위의 코드에서 앞면이 나오는 조건(x< 0.5)에서만 횟수를 늘리는 작업을 수행하므로 else는 필요가 없다.

  2. 반복문 for 문 뒤에 반복적으로 수행할 문장들(블럭)은 모두 들여쓰기를 해주어야 한다.

  3. 또한 if 문 뒤에 조건에 따라서 수행할 문장들(블럭)도 들여쓰기를 해주어야 한다.

5.3.6.2. 투자 실험#

이제 조금 다른 실험을 해보자.

  • 나는 1,000,000원 을 가지고 있다.

  • 내가 구입한 금융상품은 KOSPI 주식 중에 하루마다 주식 종목을 임의로 선택해서 주식 가격이 전날에 비해 오르면 10,000원을 벌고, 내려가면 10,000원을 잃는다.

  • 임의로 선택한 주식 종목이 전날에 비해 올라갈 확률은 0.55 로 볼 수 있다.

  • 난 1년 내로 얼마나 벌 수 있을까?

이제 위에서 배운 난수, 조건문, 반복문을 이용하여 일년 후 나의 잔고에 대한 확률실험을 해보자.

다음 코드를 반복해서 실행하면서 여러분이 번 돈이 얼마나 될 지 상상해보자. 유의할 점은 날마다 임의로 선택한 주식 종목이 전날에 비해 올라갈 사건은 우연성이 있기 때문에 코드를 실행할 때 마다 결과가 다르게 나온다.

My_money = 1000000
Number_of_days = 365

for i in np.arange(Number_of_days) :

  x = np.random.rand(1)

  if x < 0.55 :
    My_money = My_money + 10000
  else : 
    My_money = My_money - 10000

My_money

1370000

더 나아가서 여러분과 같이 백만원을 가지고 이 투자상품과 동일한 확률적 성질을 가지는 금융상품에 투자한 사람이 1000 명이라고 하자. 투자한 사람들의 1년 후 잔고는 어떤 분포를 가질까?

  • 여기서 투자상품과 동일한 확률적 성질을 가졌다는 의미는 모든 금융상품의 가격이 전날에 비해 올라갈 확률이 0.55 이라는 것이다.

또한, 비현실적이지만 여기서 두 가지 가정을 하고 모의실험을 진행합니다.

  • 서로 다른 금융 상품은 서로 영향을 주지 않다는 것을 가정합니다.

  • 금융상품 가격의 변동이 과거의 가격에 영향을 받지 않는다고 가정합니다.

실제는 많은 금융 상품들이 서로의 가격에 영향을 주고, 과거의 가격이 미래의 가격 변동에 영향을 미치는 것이 사실입니다. 하지만 문제를 단순하게 만들기 위하여 이러한 가정을 하는 것입니다.

먼저 다음과 같이 초기 변수를 정의하자.

  • 초기 투자 금액: My_money

  • 투자자의 수: Number_of_people

  • 투자 일수: Number_of_days

  • 임의로 선택한 주식 종목이 전날보다 오를 확률 : P

My_money = 1000000      # 초기 투자 금액
Number_of_people = 1000 # 투자자의 수
Number_of_days = 365    # 투자 일수

P = 0.55 # 주식 종목이 전날보다 오를 확률

투자자들의 초기 금액의 저장된 벡터를 People_money 로 만들자.

명령어 np.repeat(a,n)은 동일한 값 a를 가진 길이 n 의 벡터를 만드는 명령문이다.

# 투자자들의 초기 금액의 저장된  벡터
People_money = np.repeat(My_money, Number_of_people )  

People_money[0:10]

array([1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000,
       1000000, 1000000, 1000000])

이제 1000명의 투자자들이 각각 365일동안 투자를 한 후에 잔고를 구하는 코드를 아래와 같이 작성해 보자.

아레 코드의 특징은 두 개의 반복문을 중첩해서 사용한 것이다.

먼저 투자일 i 를 선택하고, 다음 투자자 j 마다 임의로 선택한 주식의 가격에 대한 결과를 투자 금액 People_money[j]에 반영하였다.

  • 1차 반복에서 투자일 선택: for i in np.arange(Number_of_days)

    • 2차 반복에서 투자자 선택: for j in np.arange(Number_of_people)

      • 임의로 선택한 주식의 결과 x 에 따라서 j 번째 투자자의 금액 업데이트

for i in np.arange(Number_of_days) :

  for j in np.arange(Number_of_people) :

    x = np.random.rand(1)

    if x < P :
      People_money[j] = People_money[j] + 10000
    else : 
      People_money[j] = People_money[j] - 10000

이제 1000명 투자자들의 1년 후 잔고 People_money 를 요약해 보자.

1000명의 잔고 금액를 우리가 배운 데이터프레임으로 변환한 뒤에 요약통계량과 분포를 살펴보자.

df = pd.DataFrame({ 'money': People_money})
df.head(10)
money
0 1630000
1 970000
2 1250000
3 1190000
4 1450000
5 1410000
6 1430000
7 1530000
8 1110000
9 1550000 
df.describe()
money
count 1.000000e+03
mean 1.359400e+06
std 1.899045e+05
min 6.300000e+05
25% 1.230000e+06
50% 1.370000e+06
75% 1.490000e+06
max 1.910000e+06 
df['money'].plot.hist(bins=20)

<matplotlib.axes._subplots.AxesSubplot at 0x7fd630a9cf10>
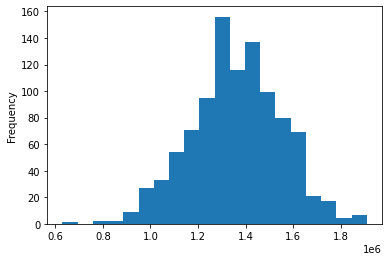
../../_images/cacc365b51b94985e8d744f54764db42bdf821f654e62e9dd53080a72b4d0248.png

1년간 투자 후에 원금 100만원보다 적은 잔고를 가진 사람, 즉 투자에서 손실을 본 사람은 몇 명인가?

df[df["money"] < My_money ].count()

money    33
dtype: int64

다행히 손실을 본 사람의 수는 많지 않다. 그 이유는 임의로 선택한 종목의 주가가 오를 확률을 낙관적으로(P=0.55)로 설정했기 때문이다. 여러분이 위의 코드를 실행한 결과는 이 노트에 있는 숫자와 다를 수 있다. 왜냐하면 코드를 실해했을 때 난수의 결과가 다르기 때문이다.

이제 초기투자 금액, 투자 기간, 코스피가 오르는 확률 등을 초기값들을 바꾸어 가면서 투자 실험을 해보자.

투자 기간(일, Number_of_days )과 투자자의 수(명,Number_of_people)을 곱한 횟수가 실험의 총 반복수이다. 총 반복수가 클수록 실행시간도 오래 걸린다.

My_money = 500000      # 초기 투자 금액
Number_of_people = 1000 # 투자자의 수
Number_of_days = 365*2  # 투자 일수

P = 0.45 # 임의로 선택한 주식의 가격이 전날보다 오를 확률

# 투자자들의 초기 금액의 저장된  벡터
People_money = np.repeat(My_money, Number_of_people )  

# 투자 실험
for i in np.arange(Number_of_days) :   
  for j in np.arange(Number_of_people) :   

    x = np.random.rand(1)

    if x < P :
      People_money[j] = People_money[j] + 10000
    else : 
      People_money[j] = People_money[j] - 10000

# 최종 잔고를 데이터프레임으로 
df = pd.DataFrame({ 'money': People_money})

df.describe()
money
count 1.000000e+03
mean -2.210600e+05
std 2.710586e+05
min -1.080000e+06
25% -4.000000e+05
50% -2.200000e+05
75% -4.000000e+04
max 6.000000e+05 
df[df["money"] < My_money ].count()

money    997
dtype: int64

df['money'].plot.hist(bins=20)

<matplotlib.axes._subplots.AxesSubplot at 0x7fd630287310>
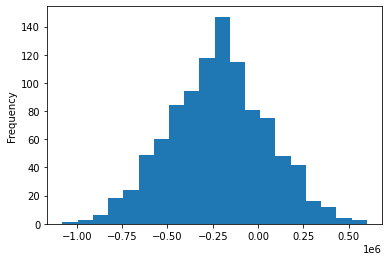
../../_images/6c725dac42752e062b71e43963f6ff1a6a52c0e1dd6ded13c52de5f5abb92e84.png

위에서 우리가 구현해 본 확률 실험은 현실성이 떨어지는 투자 방법을 가정하였다. 사람들은 투자할 주식의 종목을 임의로 랜덤하게 선택하지는 않을 것이다. 하지만 앞에서 구현한 확률 실험는 금융에서 사용되는 다양한 상품들에 대하여 위험성을 알아 보는 복잡한 실제 실험의 기본적 구조를 제공한다.

초기 조건을 다양하게 바꾸어 보아도 사람들의 최종 투자 금액의 분포를 보면 평균에서 대칭인 정규분포와 매우 유사한 것을 알 수 있다. 앞 절에서 배운 정규분포는 신장이나 몸무게 등의 분포 모양을 설명하기 위하여 수학적으로 만든 분포가 아니다.

여러분이 위에서 본 것처럼 간단한 실험에서 투자 잔고의 분포는 정규분포와 매우 유사하게 나타난다. 실제로 투자하는 날의 수를 증가시키면 최종 잔고의 분포는 정규분포와 더욱 가까워 진다.