자료의 분포 연습: 요약 통계량의 정의, 정규분포#
https://www.chosun.com/international/china/2022/10/16/PS34GVMYRZCOFGJRLPWUDFVHU4/import pandas as pd
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
%matplotlib inline
/Users/ylee19067/opt/anaconda3/lib/python3.8/site-packages/scipy/__init__.py:146: UserWarning: A NumPy version >=1.16.5 and <1.23.0 is required for this version of SciPy (detected version 1.23.1
warnings.warn(f"A NumPy version >={np_minversion} and <{np_maxversion}"
자료의 분포를 나타내는 요약 통계량#
자료의 중심을 나타내는 대표값
평균 (mean, average)
중간값 (중위수, median)
중간값의 계산
자료를 순서대로 늘어놓았을 때 중간에 오는 값
자료의 길이 n이 홀수이면 (n + 1)/2번째의 값이고
자료의 길이 n이 짝수이면 n/2번째의 값과 n/2 + 1번째 값의 평균이다.
자료의 극단(extreme)을 나타내는 대표값
최소값과 최대값
자료의 퍼진 정도를 나타내는 대표값
하위 50% 집단의 중간값 (아래 4분위수: Q1) => 1/4 번째 수
상위 50% 집단의 중간값 (위 4분위수: Q3) => 3/4 번째 수
k 번째 수의 순서: (k-1)/(n-1) 번째
4분위수 거리 (IQR, inter-quanrtile range; inter-quantile range)
IQR = Q3 − Q1
예제 1#
1,2,3,4,5,6,7,8,9,10
Q1?
n = 10 이므로 3 는 (3 -1 )/(10-1) = 2/9 번째 수
n = 10 이므로 4 는 (4 -1 )/(10-1) = 3/9 번째 수
Q1 = 1/4 번째 수
따라서
\[ Q1 = 3\frac{(3/9-1/4)}{(3/9-2/9)} + 4\frac{(1/4-2/9)}{(3/9-2/9)} = 3.25 \]Q3?
n = 10 이므로 7 는 (7 -1 )/(10-1) = 6/9 번째 수
n = 10 이므로 8 는 (8 -1 )/(10-1) = 7/9 번째 수
Q1 = 3/4 번째 수
따라서
\[ Q3 = 7 \frac{(7/9-3/4)}{(7/9-6/9)} + 8\frac{(3/4-6/9)}{(7/9-6/9)} = 7.75 \]
x = np.array([1,2,3,4,5,6,7,8,9,10])
x
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
(x-1)/(len(x)-1) # 순서
array([0. , 0.11111111, 0.22222222, 0.33333333, 0.44444444,
0.55555556, 0.66666667, 0.77777778, 0.88888889, 1. ])
df1 = pd.DataFrame({'x': x})
df1
| x | |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
| 4 | 5 |
| 5 | 6 |
| 6 | 7 |
| 7 | 8 |
| 8 | 9 |
| 9 | 10 |
df1.describe()
| x | |
|---|---|
| count | 10.00000 |
| mean | 5.50000 |
| std | 3.02765 |
| min | 1.00000 |
| 25% | 3.25000 |
| 50% | 5.50000 |
| 75% | 7.75000 |
| max | 10.00000 |
예제 2#
1,2,3,4,5,6,7,8,9
Q1?
n = 9 이므로 3 는 (3 -1 )/(9-1) = 2/8 = 1/4 번째 수
Q1 = 1/4 번째 수
따라서 Q1 = 3
Q3?
n = 9 이므로 7 는 (7 -1 )/(9-1) = 6/8 = 3/4 번째 수
Q3 = 3/4 번째 수
따라서 Q3 = 7
x=np.array([1,2,3,4,5,6,7,8,9])
(x-1)/(len(x)-1) # 순서
array([0. , 0.125, 0.25 , 0.375, 0.5 , 0.625, 0.75 , 0.875, 1. ])
df2 = pd.DataFrame({'x': x})
df2
| x | |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
| 4 | 5 |
| 5 | 6 |
| 6 | 7 |
| 7 | 8 |
| 8 | 9 |
df2.describe()
| x | |
|---|---|
| count | 9.000000 |
| mean | 5.000000 |
| std | 2.738613 |
| min | 1.000000 |
| 25% | 3.000000 |
| 50% | 5.000000 |
| 75% | 7.000000 |
| max | 9.000000 |
상자그림#
자료의 분포을 나타내는 그림
box plot
위 선 끝점: Q3 + (1.5)IQR
상자 위: 75% 백분위수 (3사분위수, Q3)
상자 중앙: 중앙값(median)
상자 아래 : 25% 백분위수 (1사분위수, Q1)
아래 선 끝점: Q1 - (1.5)IQR
y = np.random.rand(50)
df3 = pd.DataFrame({'y':y})
boxplot = df3.plot.box(y='y')
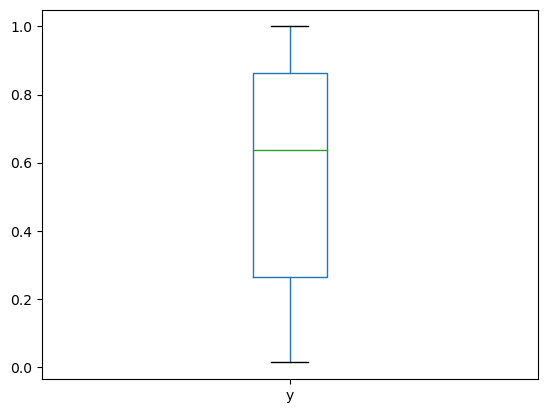
이상점#
이상점, 특이값 (outlier)
자료의 값들 중 전체적인 경향에서 벗어난 값
이상점은 잘못된 값일 수도 있으나 (예: 입력오류) 자료의 일부분인 경우도 흔하다 (예: 대한민국 국가대표의 연봉 중 손흥민의 연봉)
이상점의 판별 - 매우 어려움
이상점이 존재하는 경우 자료의 요약에 대하여 세심한 주의를 기울여야 한다 (예: median의 사용)
다음 두 자료 의 평균과 중앙값은?
자료1: 1, 2, 3, 4, 5
자료2: 1, 2, 3, 4, 100
매우 특이한 값이 존재하거나 자료가 매우 비대칭일 경우 중심의 측도로서 평균은 적절치 않다.
정규분포#
평균 \(\mu\)이고 분산이 \(\sigma^2\)인 정규분포를 \(N(\mu,~\sigma^2)\)로 표시한다.
\(N(\mu,~\sigma^2)\)의 확률밀도함수
평균 \(\mu\)를 중심으로 대칭이며 꼬리의 확률이 빠르게 줄어드는 분포
평균 0 이고 분산이 1인 정규분포는 표준정규분포 (\(N(0,1)\), standard normal distribution)
자료의 퍼진 정도가 분산 \(\sigma^2\)에 따라 다르다.
\(X\)의 분포가 \(N(\mu,~\sigma^2)\)일 때 \(Z=(X-\mu)/\sigma\)의 분포는 \(N(0,1)\)이다.
표준 정규분포의 확률밀도함수#
정규분포의 평균과 표준편차의 값은 아래 mu 와 sigma 값입니다.
참고: 아래 정규분포의 확률밀도함수를 그리는 파이썬 표현식은 시함이나 과제에 나오지 않습니다. 학생들의 이해를 돕기 위하여 그래프를 그리는 프로그램이므로 따로 공부할 필요는 없습니다.
mu=0
sigma=1
normal_distribution=stats.norm(mu,sigma)
heights=np.linspace(mu-3*sigma, mu+3*sigma,10000)
plt.plot(heights,normal_distribution.pdf(heights),'b')
[<matplotlib.lines.Line2D at 0x7ff240f09430>]
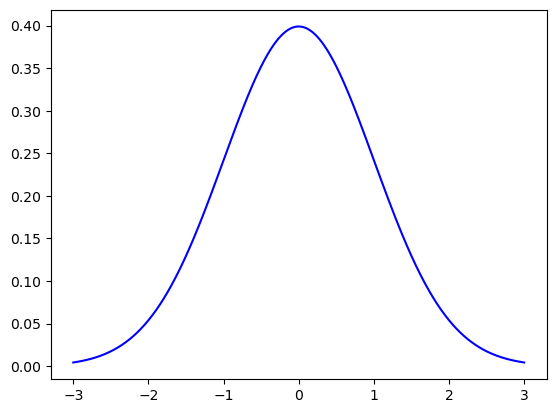
정규분포의 확률 계산#
\(X\)의 분포가 \(N(\mu,~\sigma^2)\)일 때, 임의의 \(a<b\) 에 대하여
정규분포의 성질#
\(X\)의 분포가 \(N(\mu,~\sigma^2)\)일 때
\begin{eqnarray*} P( \mu-\sigma <X<\mu+\sigma) =& 0.683 \quad \text{(blue area)}\ P( \mu-2\sigma <X<\mu+2\sigma) =& 0.954 \quad \text{(green area)}\ P( \mu-3\sigma <X<\mu+3\sigma) =& 0.995 \quad \text{(red area)} \end{eqnarray*}
normal_distribution.cdf(mu+sigma) - normal_distribution.cdf(mu-sigma)
0.6826894921370859
normal_distribution.cdf(mu+2*sigma) - normal_distribution.cdf(mu-2*sigma)
0.9544997361036416
normal_distribution.cdf(mu+3*sigma) - normal_distribution.cdf(mu-3*sigma)
0.9973002039367398
heights=np.linspace(mu-4*sigma, mu+4*sigma,10000)
plt.plot(heights,normal_distribution.pdf(heights),'b')
area=np.arange(mu-sigma,mu+sigma ,0.1)
plt.fill_between(area,normal_distribution.pdf(area),color='b')
<matplotlib.collections.PolyCollection at 0x7ff1d035e5e0>
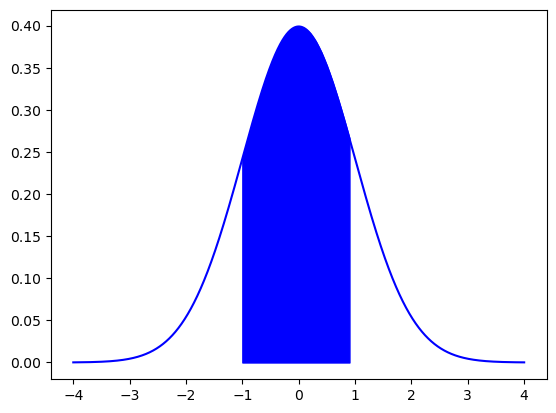
heights=np.linspace(mu-4*sigma, mu+4*sigma,10000)
plt.plot(heights,normal_distribution.pdf(heights),'b')
area=np.arange(mu-2*sigma,mu+2*sigma ,0.1)
plt.fill_between(area,normal_distribution.pdf(area),color='g')
<matplotlib.collections.PolyCollection at 0x7ff210725f70>
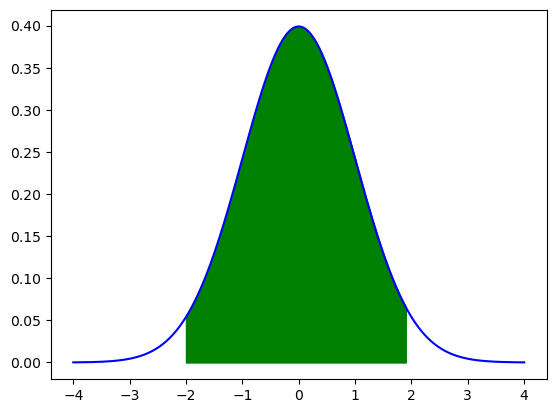
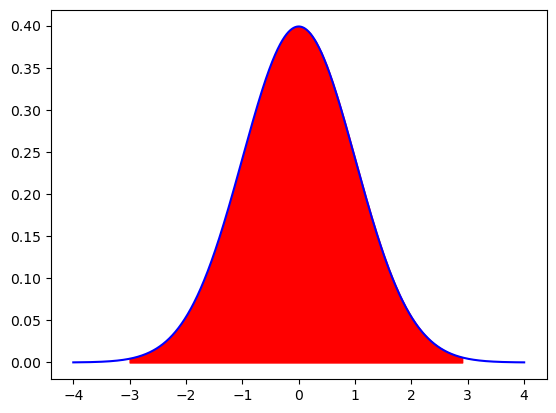
heights=np.linspace(mu-4*sigma, mu+4*sigma,10000)
plt.plot(heights,normal_distribution.pdf(heights),'b')
area=np.arange(mu-3*sigma,mu+3*sigma ,0.1)
plt.fill_between(area,normal_distribution.pdf(area),color='r')
<matplotlib.collections.PolyCollection at 0x7ff1d0413af0>
정규분포에서 난수 추출#
라이브러리 numpy 의 np.random.normal(mu, sigma, n) 함수를 사용한다.
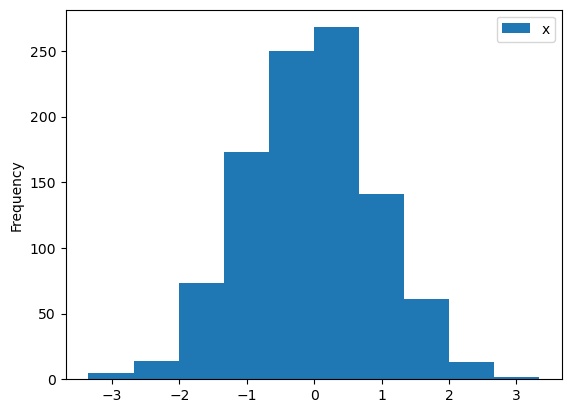
df3= pd.DataFrame({'x': np.random.normal(mu, sigma, 1000)})
df3.plot.hist(y='x')
<AxesSubplot:ylabel='Frequency'>
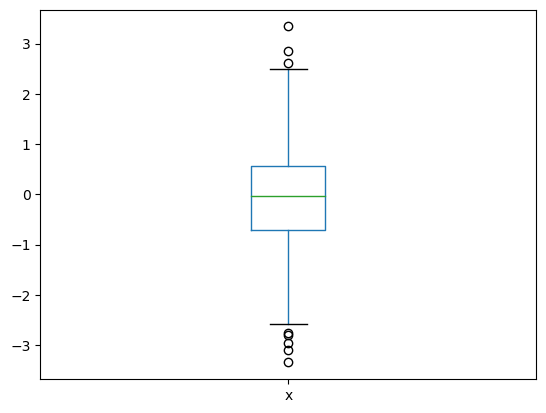
df3.plot.box(y='x')
<AxesSubplot:>
df3.describe()
| x | |
|---|---|
| count | 1000.000000 |
| mean | -0.054477 |
| std | 0.970082 |
| min | -3.348352 |
| 25% | -0.713155 |
| 50% | -0.035265 |
| 75% | 0.569991 |
| max | 3.340564 |

